推荐在日间模式下阅读

命名实体识别(NER)

命名实体识别属于自然语言处理中的序列标注任务，是指从文本中识别出特定命名指向的词，比如人名、地名和组织机构名等。具体而言，输入自然语言序列 ，给出对应标签序列 ，见下图。

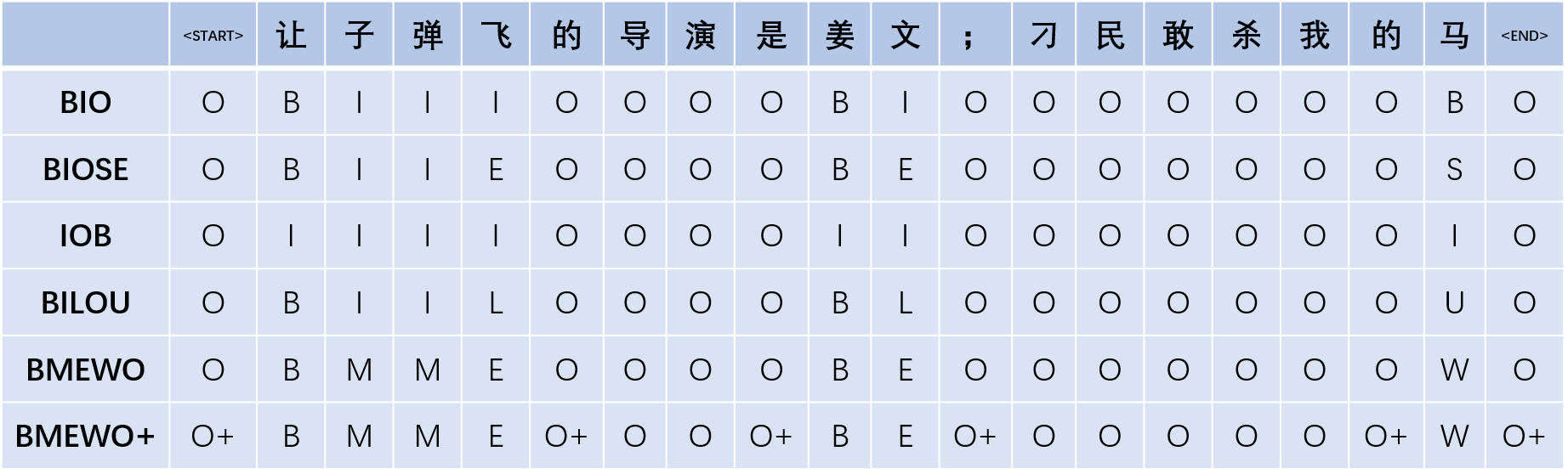
序列标注里标记法有很多，包括BIO、BIOSE、IOB、BILOU、BMEWO、BMEWO+等，最常见的是 BIO 与 BIOES 这两种。不同标注方法会对模型效果有些许影响，例如有些时候用BIOES会比BIO有些许优势。

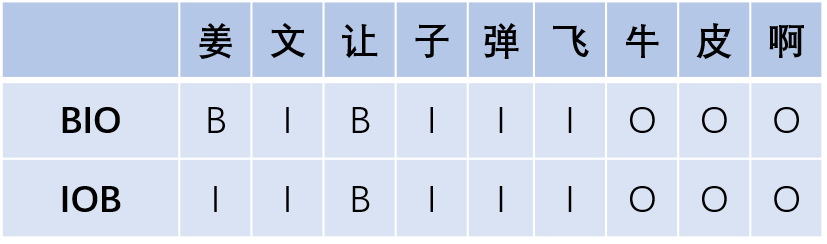
在BIO和BIOSE中，Beginning 表示某个实体词的开始，Inside表示某个实体词的中间，Outside表示非实体词，End表示某个实体词的结尾，Single表示这个实体词仅包含当前这一个字。IOB与BIO字母对应的含义相同，其不同点是IOB中，标签B仅用于两个连续的同类型命名实体的边界区分。BILOU 等价于 BIOES，Last等同于End，Unit等同于Single。BMEWO 等价于 BIOES，Middle等同于Inside，Whole等同于Single。BMEWO+是在命名实体边界外的标注，即‘ O plus ‘。

命名实体识别的常用方法是BiLSTM-CRF和BERT-CRF，可以完美的匹配该任务。

BiLSTM-CRF模型

下文，我们使用BIO标注进行解析，同时加入START和END来使转移矩阵更加健壮，其中，START表示句子的开始，END表示句子的结束。这样，标注标签共有5个：[B, I, O, START, END]。

BiLSTM-CRF模型主体由双向长短时记忆网络（Bi-LSTM）和条件随机场（CRF）组成，模型输入是字符特征，输出是每个字符对应的预测标签。

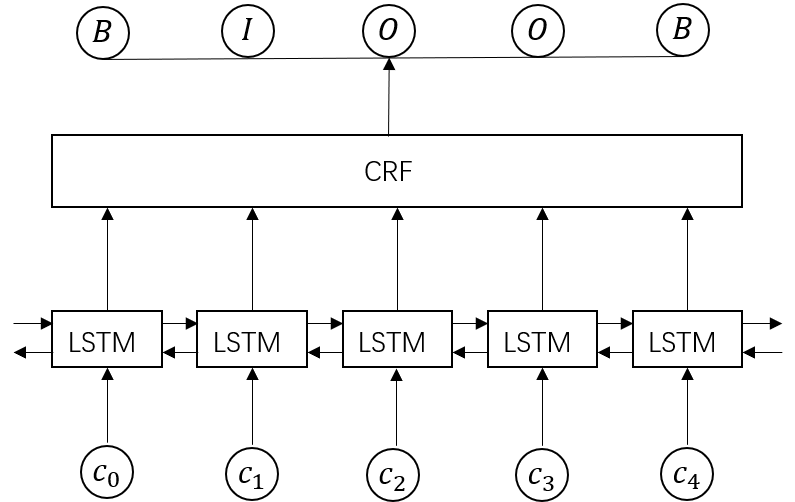
模型输入

对于输入的自然语言序列，可通过特征工程的方法定义序列字符特征，如词性特征、前后词等，将其输入模型。但现在多数情况下，可以直接选择句中每个字符的字嵌入或词嵌入向量，可以是事先训练好的或是随机初始化。对于中文，一般倾向于将字符向量和其所属的词向量进行拼接，词嵌入使用预训练好的，字嵌入随机初始化。

LSTM

BiLSTM接收每个字符的embedding，并预测每个字符的对5个标注标签的概率。

LSTM是一种特殊的循环神经网络，可以解决RNN的长期依赖问题，其关键就是细胞状态，见下图中贯穿单元结构上方的水平线。细胞状态在整个链上运行，只有一些少量的线性交互，从而保存长距离的信息流。具体而言，LSTM一共有三个门来维持和调整细胞状态，包括遗忘门，输入门，输出门。

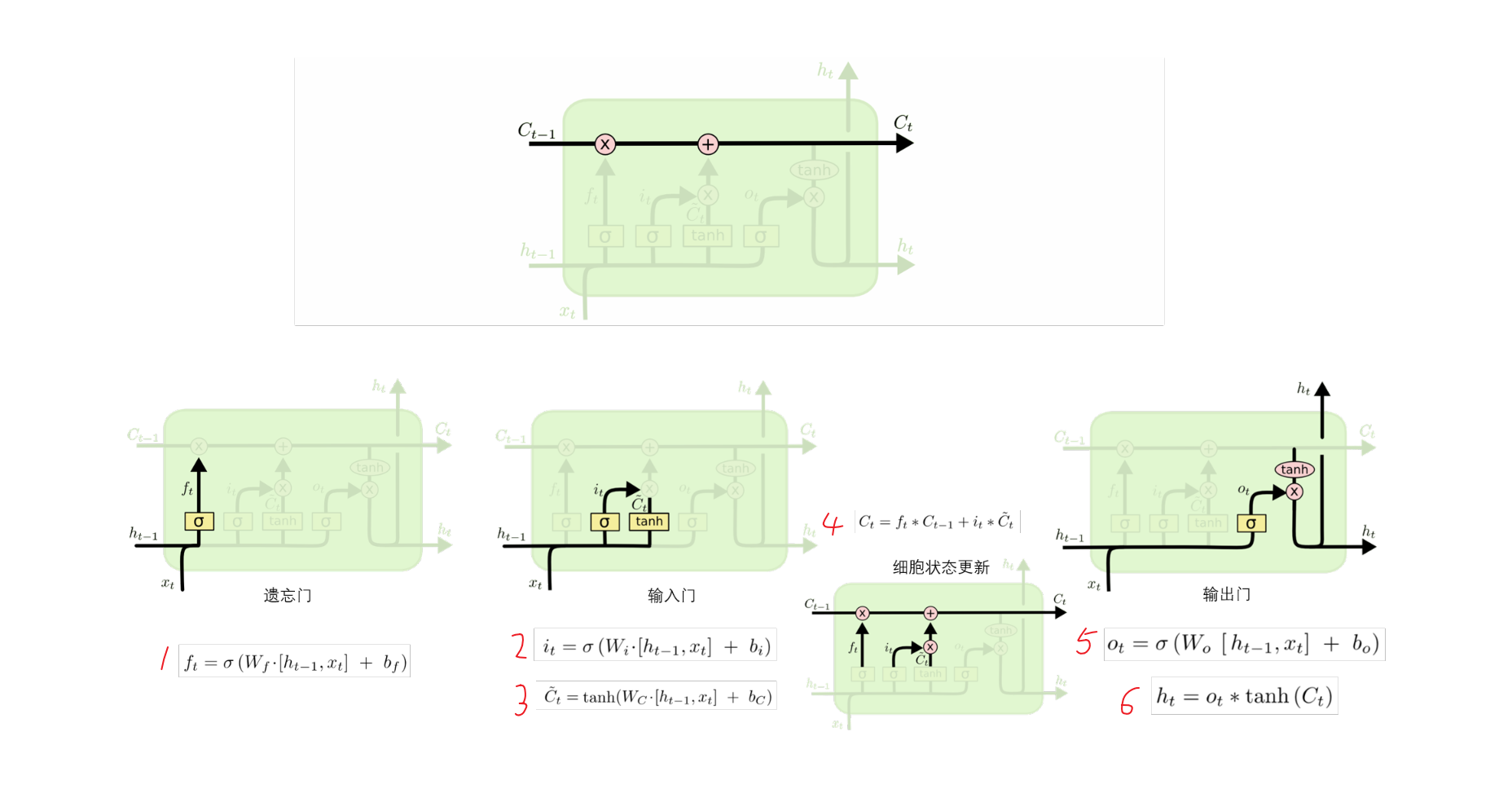
遗忘门接受$h_{t-1}$和$x_t$,通过公式1输出一个0到1之间的数值$f_t$,这个数值会作用于上一个细胞状态$C_{t-1}$,1表示“完全保留”，0表示”完全忘记”；输入们接受$h_{t-1}$和$x_t$,通过公式2输出一个0到1之间的数值，以控制当前候选状态$\hat{C_t}$又多少信息需要保留,至于候选状态$\hat{C_t}$，则通过公式2由tanh层创建一个新的候选值向量，然后根据上一个细胞状态$C_{t-1}$和遗忘值$f_t$、新的细胞状态$C_the$输入值$i_t$，由公式4更新细胞状态；输出门接受$h_{t-1}$和$x_t$，通过公式5输出一个在0到1之间的数值$o_t$,最后公式6决定了当前状态$C_t$有多少信息需要输出。

题外话：LSTM的理解

一般来说，循环神经网络是MLP增加了一个时间维度，那么该怎样理解这个时间维度呢？可以参考以下两张图可视化LSTM。

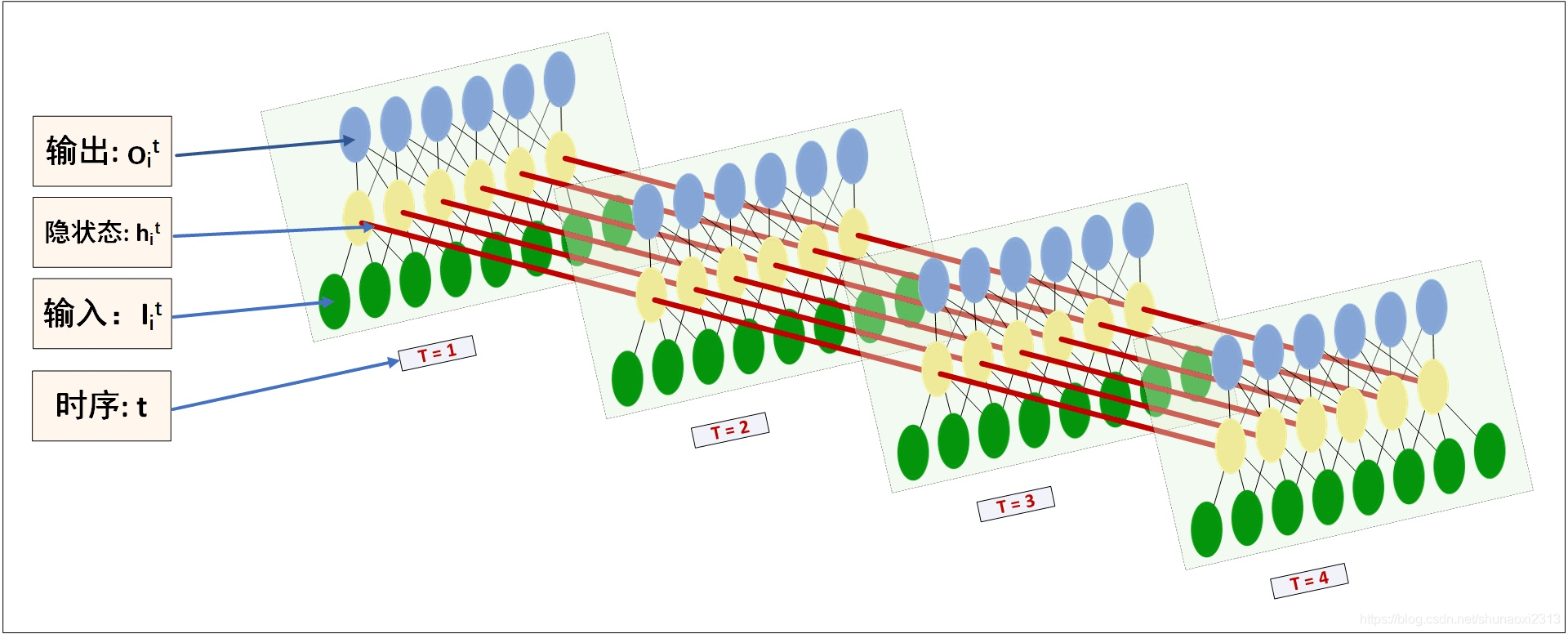
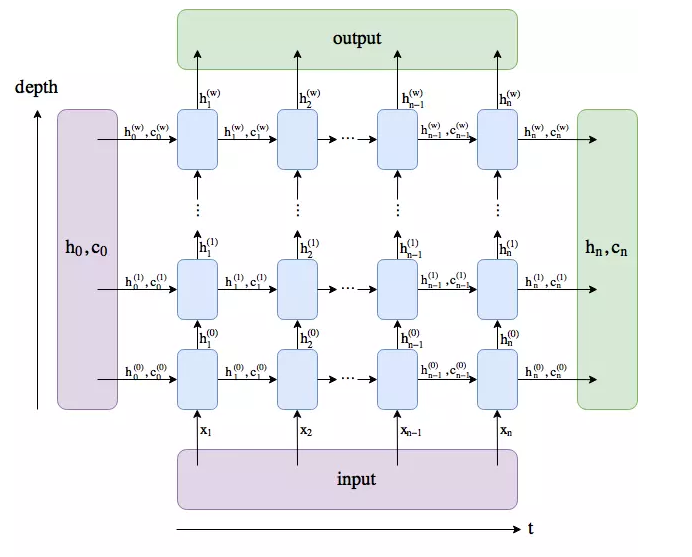
在$torch.nn.LSTM()$中，有以下几个重要的参数

  • $input$_$size$：是每个字符嵌入的维度。
  • $hidden$_$size$：经过一个LSTM单元后输入h的维度。
  • $num$_$layers$：即上图中depth的深度，若干个LSTMcell的堆叠
  • $bidirectional$：默认False

LSTM的输入包括$input$和$(h_0,c_0)$两部分，其中$input$大小为$(seq_len, batch, input_size)$，$h_0$和$c_0$大小均为$(num_layersnum_directions, batch, hidden_size)$。输出包括$output$和$(h_n, c_n)$两部分，其中$output$大小为$(seq_len, batch, num_direction hidden_size)$，$h_n$和$c_n$大小均为$(num_layers*num_direction, batch, hidden_size)$。

我们知道，CNN在空间上共享参数，而RNN是在时间上共享参数。也就是在每一层depth中只有一个LSTMcell，即上面第二张图中每一层只有一个LSTM单元。

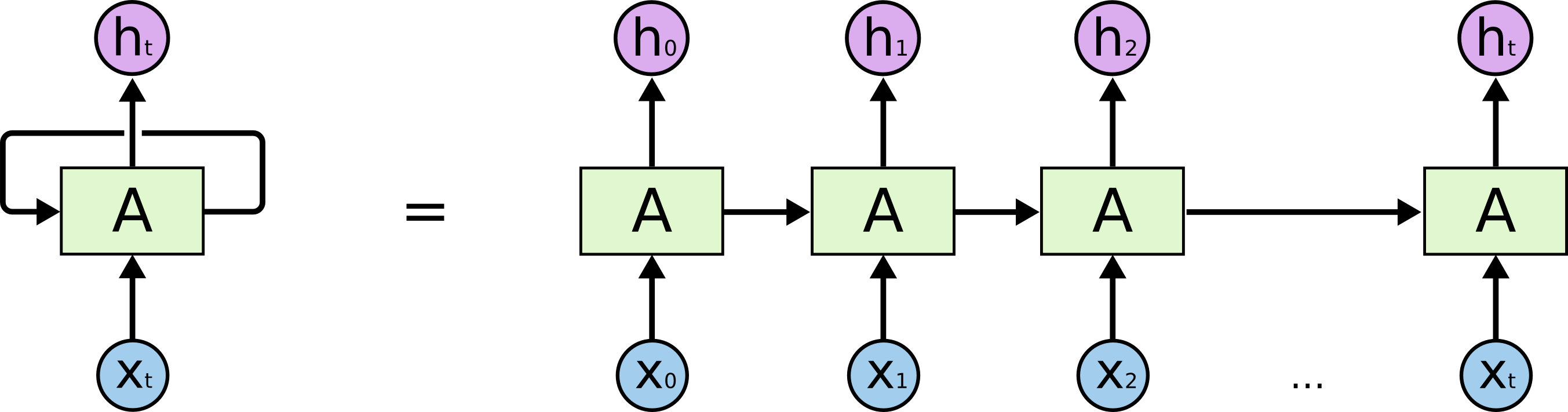
继续…

在BiLSTM-CRF中，一般使用一层的双向LSTM是足够的。因此，BiLSTM对输入embeddings的特征提取过程如下图。

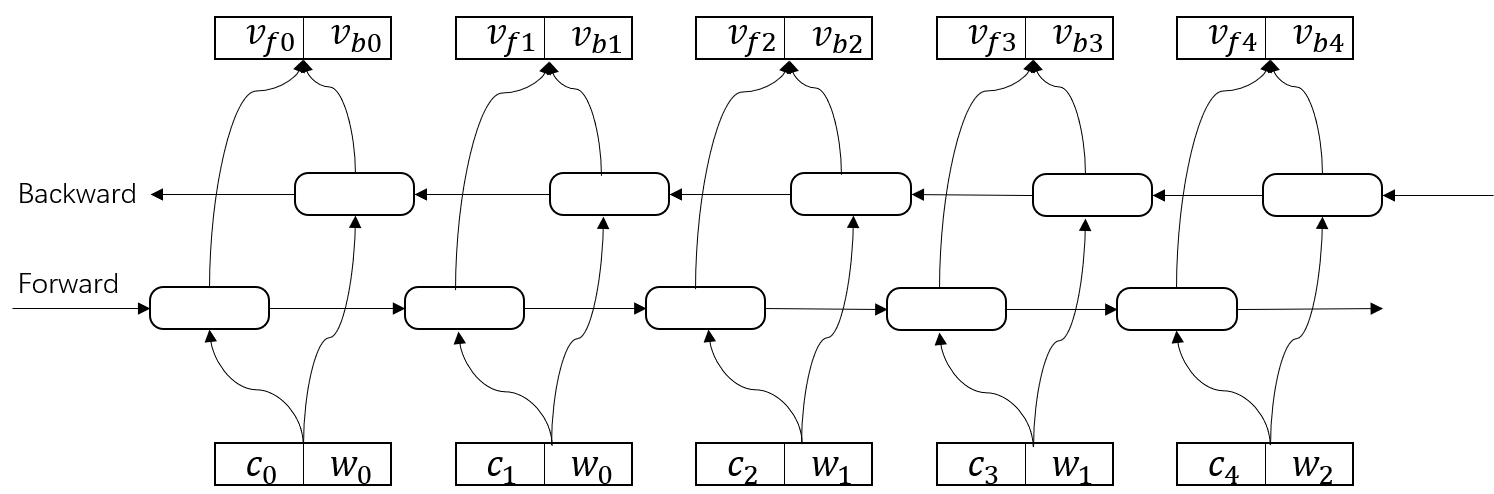
本部分一开始就说过，BiLSTM接收每个字符的embedding，并预测每个字符的对5个标注标签的概率。但是，我们也知道上图得到的拼接向量维度大小为[num_directions, hidden_size]。为将输入表示为字符对应各个类别的分数，需要在BiLSTM层加入一个全连接层，通过softmax将向量映射为一个5数值的分布概率。（注：此处也可不加softmax激活函数，直接使用全连接层映射为一个5数值分布即可，区别仅在于得到的emission score值大小及该维加和是否等于1。下图示表示使用了softmax，可见各列加和为1）

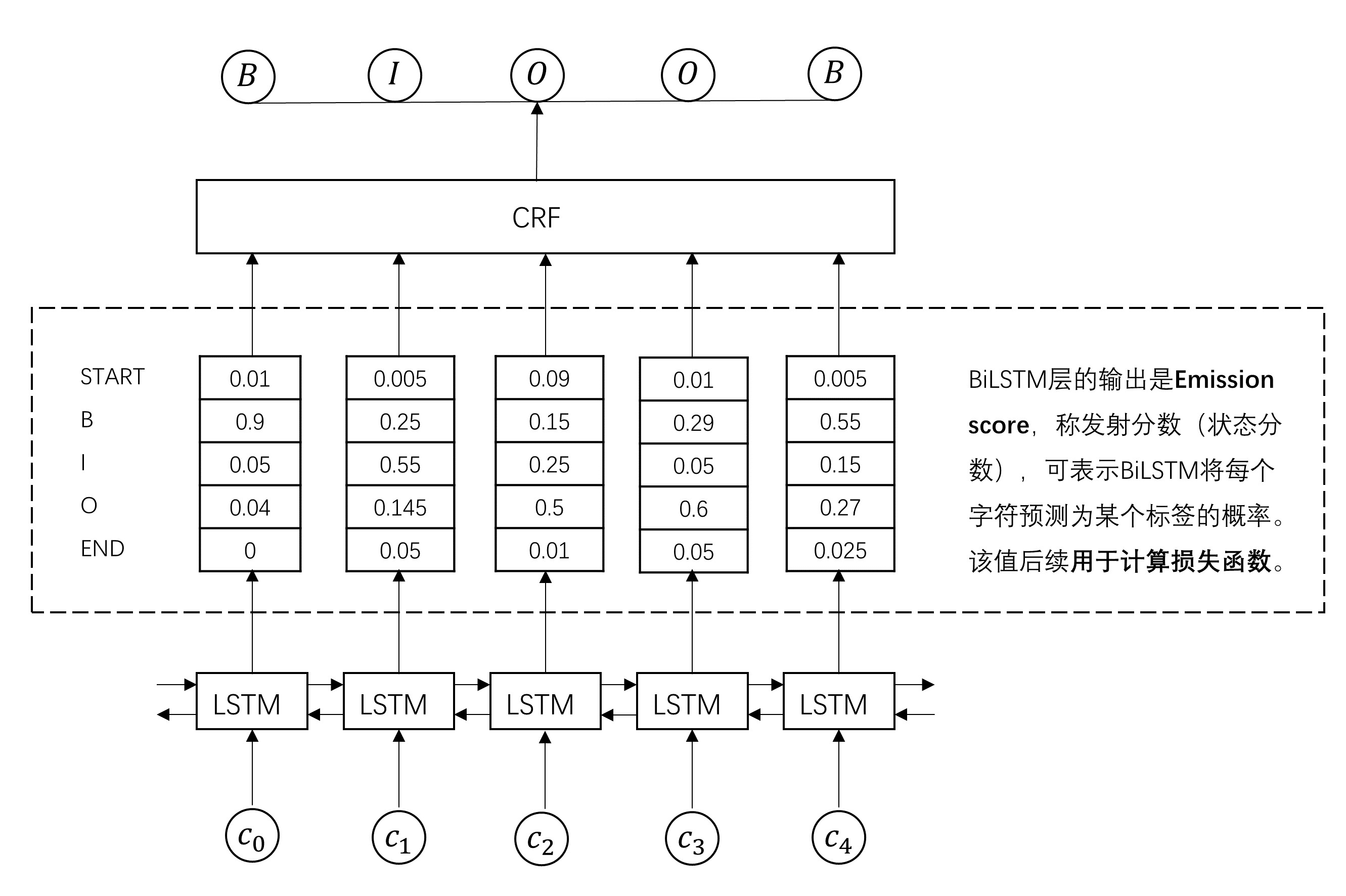
到了这一步，似乎通过BiLSTM已经找到每个单词对应的最大标签类别，但实际上，直接选择该步骤最大概率的标签类别得到的结果并不理想。原因在于，尽管LSTM能够通过双向的设置学习到观测序列之间的依赖，但softmax层的输出是相互独立的，输出相互之间并没有影响，只是在每一步挑选一个最大概率值的label输出，这样的模型无法学习到输出的标注之间的转移依赖关系（标签的概率转移矩阵）以及序列标注的约束条件，如句子的开头应该是“B”或“O”，而不是“I”等。为此，引入CRF层学习序列标注的约束条件，通过转移特征考虑输出label之间的顺序性，确保预测结果的有效性。

CRF

CRF层将BiLSTM的Emission_score作为输入，输出符合标注转移约束条件的、最大可能的预测标注序列。

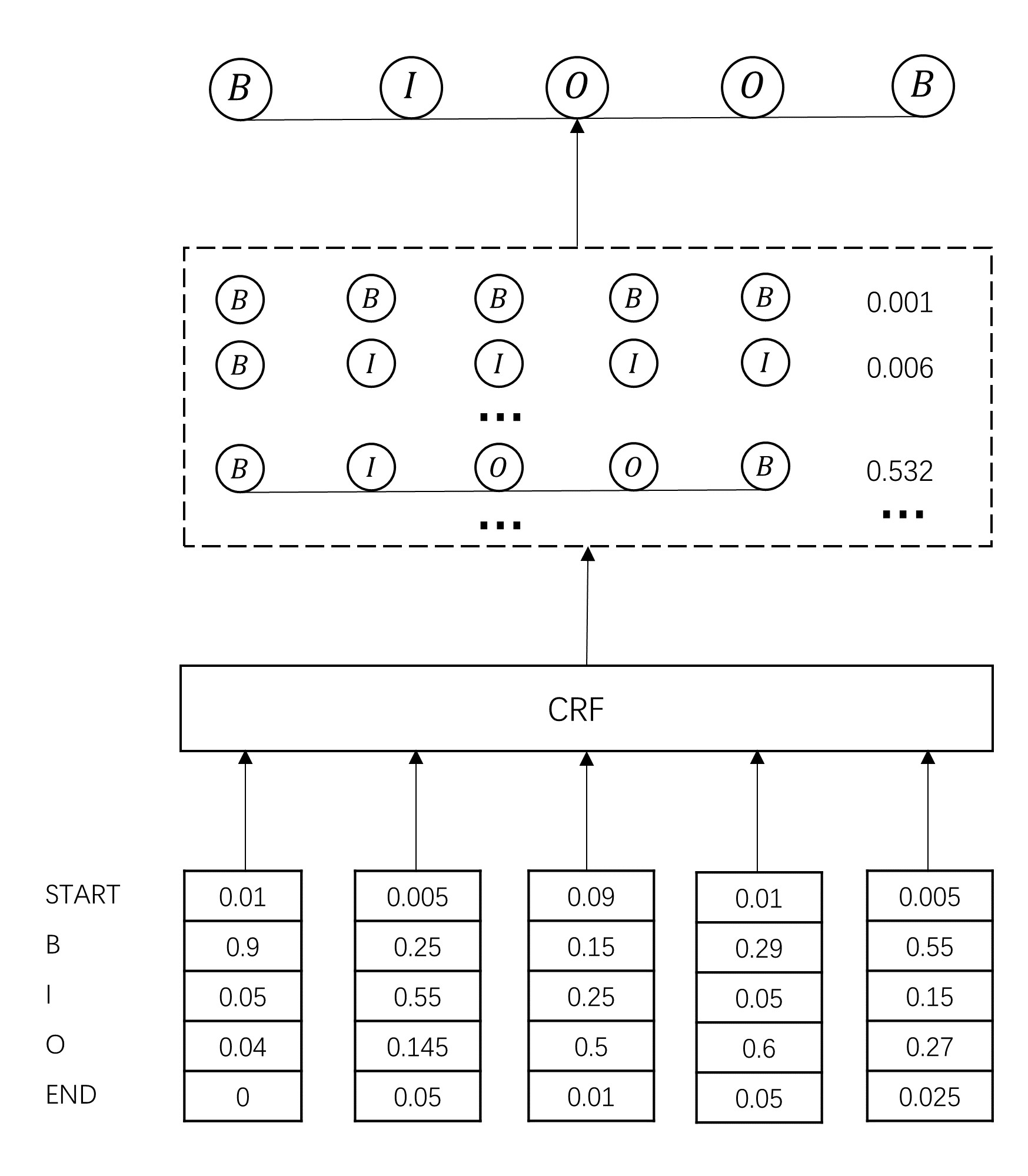
在开始之前…

先了解一下线性链条件随机场。见李航老师的《统计学习方法》第11章。

可以看到，NER问题就是条件随机场，即给定自然语言序列X，最大概率的标注序列Y用来表示NER标注结果，至于$P(y|x)$，由公式(11.10)和(11.11)求得。

上图中标出、公式(11.10)有三个值得注意的部分：$t_k$，$s_l$和$Z(X)$，理解这三个部分是理解BiLSTM-CRF模型中CRF的关键，以下图说明。

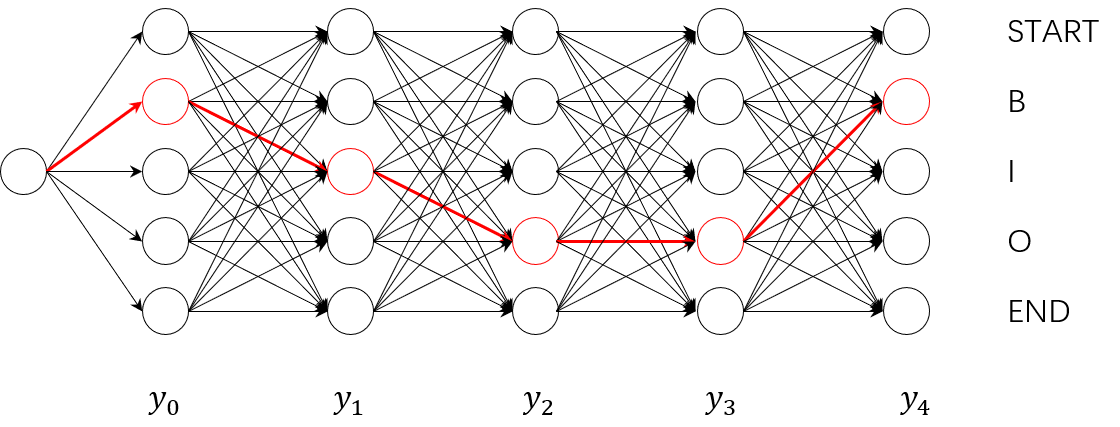
在例子中，输入$x$为$c_0,c_1,c_2,c_3,c_4$，理想输出$y$为$B,I,O,O,B$，上图中红的线路。

$Z(x)$，称为规范化因子或配分函数。在公式(11.10)中，$Z(x)$是规范化因子，求和是在所有可能的输出序列上进行的。对应到我们的图中，其实就是途中所有可能的路径的组合，由于输入序列长度为5，标注类型也为5，英雌上图中共有$5^5$条不同的路径。每条路径是根据$exp(*)$计算该路径的个扽，加和得到$Z(x)$。

$s_t$是节点上的状态特征，取决于当前节点；$t_k$是边上的转移特征，取决于当前和前一个节点。根据他们的定义，可以很自然的将他们于BiLSTM-CRF中的Emission Score和Transition Score匹配：Emission Score是由BiLSTM生成的的、对当前字符标注的概率分布；Transition Score是加入CRF约束条件的、字符标注之间的概率转移矩阵。**从这个意义上讲，BiLSTM-CRF其实就是个CRF模型，只不过用BiLSTM得到状态特征值$s_t$，用反向传播算法更新转移特征值$t_k$**。

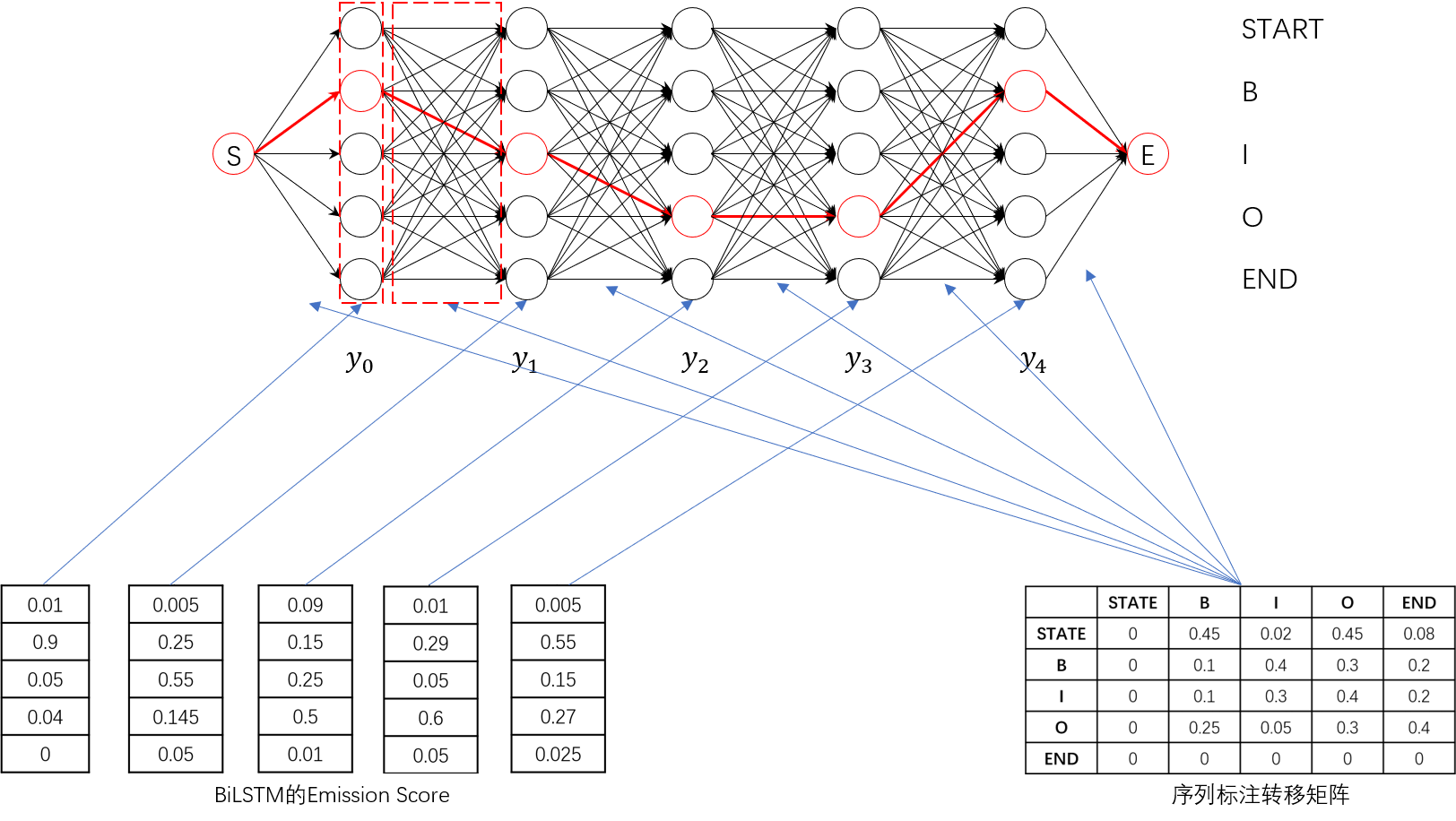
在模型训练过程中，模型损失函数定义如下：

$$P(\bar{y}|x)=\frac{exp(\operatorname{score}(x,\bar{y}))}{\sum_y{exp(\operatorname{score}(x,y))}} $$

$$ \operatorname{score}(x,y)=\sum_{i=1}^{n} P_{i, y_{i}}+\sum_{i=0}^{n} A_{y_{i-1}, y_{i}}$$

其中，**$P_{i, y_{i}}$和$A_{y_{i-1}, y_{i}}$分别表示标注序列$y$中$y_i$的Emission Score和Transition Score**，通过查找上图中的”BiLSTM的Emission Score“和”序列标注转移矩阵“可以得到每个字符位置的得分，整个序列相加得到$\operatorname{score}(x,y)$。

模型训练过程中最大化对数似然函数：

$$\log P\left(\bar{y}\mid x\right)=\operatorname{score}\left(x, \bar{y}\right)-\log \left(\sum_{y} \exp \left(\operatorname{score}\left(x, y\right)\right)\right)$$

真实路径得分

在我们的例子中，真实路径$\bar{y}=(B,I,O,O,B)$，$$\operatorname{score}(x,\bar{y})=\sum\operatorname{EmissionScores}+\sum\operatorname{TransitionScores}$$，其中：$$\sum\operatorname{EmissionScores}=P_{0,START}+P_{1, B}+P_{2, I}+P_{3,O}+P_{4, O}+P_{5,B}+P_{6,END}$$

$$ \sum\operatorname{TransitionScores}=A_{START,B}+A_{B,I}+A_{I,O}+A_{O,O}+A_{O,B}+A_{B,END}$$

EmissionScores来自BiLSTM层的输出，至于$P_{0,START}$和 $P_{6,END}$，则设为0；TransitionScores来自于CRF层；将真实路径中这两类分数加和，即可得到真实路径得分，上图中红色路线。

所有路径得分

对于所有路径的总分 $\sum_{y} \exp \left(\operatorname{score}\left(x, y\right)\right)$ ，一种直接的想法是列举出所有可能的路径，然后查找每条路径的Emission Score和Transition Score，计算出每条路径的得分，之后加和。

这种方法显然效率低下，在我们的例子中，仅有5个字符和5个标注序列，就已经有了约$5^5$种路径组合，在实际工作中，我们显然会有更长的序列和更多的标注标签，提高计算效率是必要的。于是，我们以分数累积的方法计算所有路径得分，即先计算出到达$c_0$的所有路径的总得分，然后，计算$c_0{->}c_1$的所有路径的得分，依次类推，直到计算出$c_0->c_1\dots->c_n$的所有路径的得分，这就是我们需要的结果。通过下图可以看出这两种计算方式的不同。

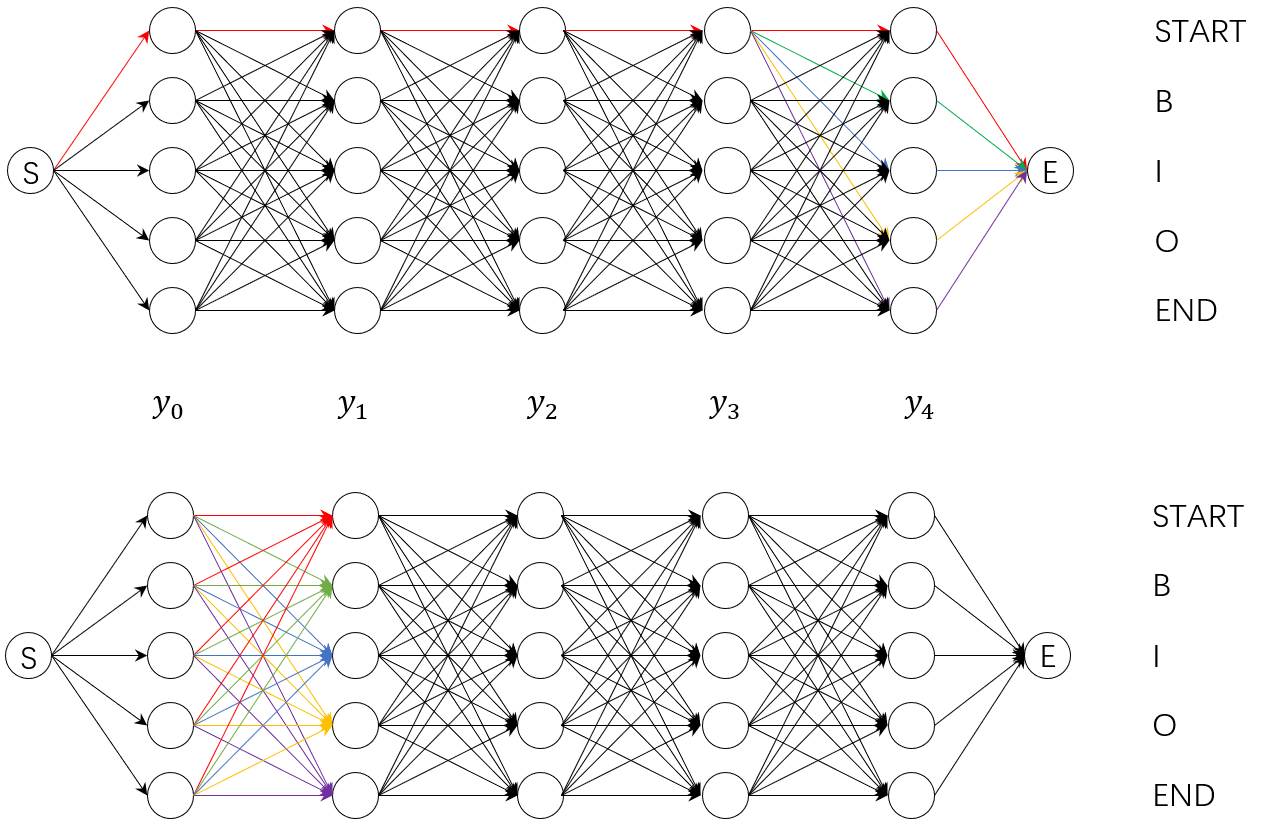
上面的图是直观的、计算所有路径得分加和的示意图，这种方法思想上是深度优先的；下面的图是改进的、分数累计求和的示意图，这种方法思想上是广度优先的。

在第一种方法中，图示以$[(S,S,S,S,S),(S,S,S,S,B),(S,S,S,S,I),(S,S,S,S,O),(S,S,S,S,E)] $五条可能的标注路径为例，每一条路径得分由该路径上节点得分（EmissionScore）和边得分（TransitionScore）相加得到，可以发现，如果计算分别计算每一条路径的话，存在大量的冗余，如对于上述五条路径，前四个标注是相同的，理论上只需分别计算最后一项不同标注即可。

分数累积的方法更为激进。要知道，在计算$Z(x) $时我们并不是要排列组合出所有可能路径，只是要一个All值，即图中所有边和节点的总值。因此，我们可以先计算出到达某一字符的路径得分之和 $(s_S^i,s_B^i,s_I^i,s_O^i,s_E^i)$，然后依次计算下一字符的路径得分之和$ (s_S^{i+1},s_B^{i+1},s_I^{i+1},s_O^{i+1},s_E^{i+1}) $，这类似于动态规划的思想，其中 $s$表示score，$$S/E$$表示标注START/END。如在上图示例中，我们在得知到达 $y_1$的路径得分之和 $(s_S^1,s_B^1,s_I^1,s_O^1,s_E^1)$后，根据 $$ s_{tag’}^2=\sum_{tags}{s_{tag}^1+t_{(tag,tag’)}}$$可分别计算出 $y_2$的路径得分之和$(s_S^2,s_B^2,s_I^2,s_O^2,s_E^2)$，图中红/绿/蓝/黄/紫分别根据$ y_1$各标注的得分计算到达 $y_2$的 $(S,B,I,O,E)$各标注的得分之和。依次类推，计算出整个图中所有路径得分之和。

在图中可以直观看到上述两种方法是等价的，其数学上的等价性见下：

$$\log \left(\sum e^{\log \left(\Sigma e^{x}\right)+y}\right)=\log \left(\sum \sum e^{x+y}\right) $$

证明过程：

$$ \begin{aligned} \log \left(\sum e^{\log \left(\Sigma e^{x}\right)+y}\right) &=\log (\sum e^{\log (\Sigma e^{x})+\log e^y}) \ &=\log (\sum e^{\log (\Sigma e^{x})*e^y})\ &=\log (\sum e^{\log (\Sigma e^{x+y})})\ &=\log \left(\sum \sum e^{x+y}\right) \end{aligned} $$

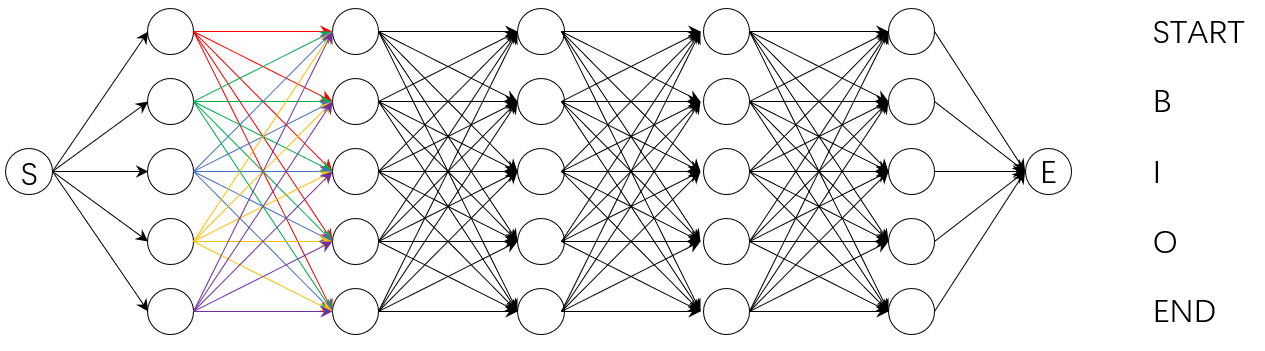
第二种方法有效减少了计算冗余。第一种方法的计算复杂度为$O（nm^n)$，其中，$m$为标注标签类别数，第二种方法的计算复杂度为$O(nm^2) $。当然，第二种方法还可以以下图这种方式计算，下文Pytorch Tutorial中的实现_forward_alg()就是如此，但本质上就是一回事。

最终BiLSTM-CRF模型如下：

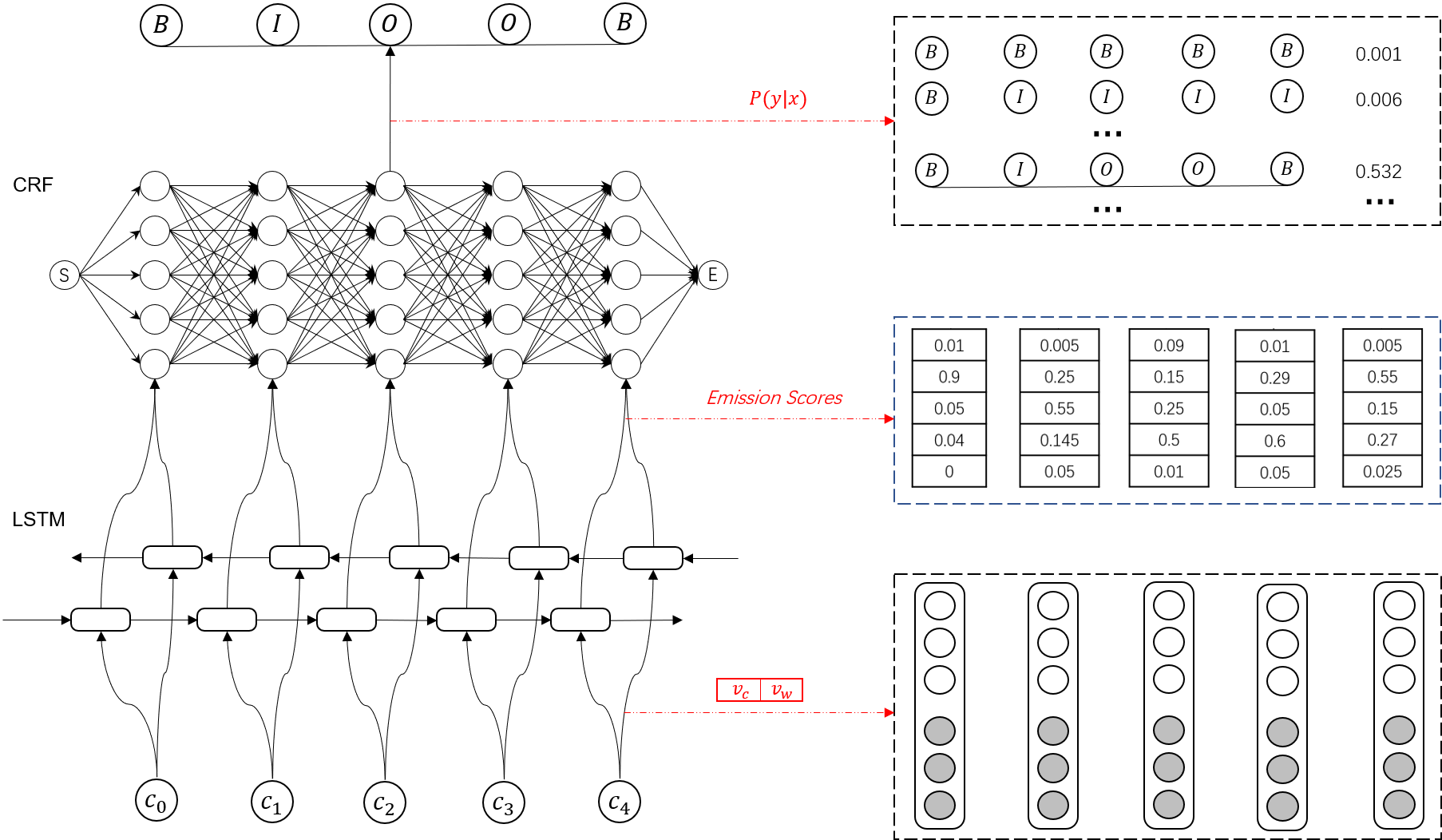
Pytorch Tutorial NER代码解析

网上多数Pytorch NER解析来自官方示例，见ADVANCED: MAKING DYNAMIC DECISIONS AND THE BI-LSTM CRF，以下代码添加有备注解析。以下几点需要注意：

  • 前文提到，模型目标是最大化对数似然函数$ \log P\left(\bar{y}\mid x\right)=\operatorname{score}\left(x, \bar{y}\right)-\log \left(\sum_{y} \exp \left(\operatorname{score}\left(x, y\right)\right)\right) $，但在深度学习中，我们一般通过最小化损失函数优化模型参数。因此，取负得到损失函数$Loss=\log (\sum_{y} \exp (\operatorname{score}(x, y)))-\operatorname{score}(x, \bar{y})$。
  • 在NER问题中，训练过程与测试过程是不同的。在训练中，我们需要计算所有路径的得分以正确更新转移矩阵，但在测试过程中，我们以然得到合理的标签概率转移矩阵，因此只需要结合Emission Score选择一条概率最大的路径。该过程为解码过程，采用Vertibe算法，参见如何通俗地讲解 viterbi 算法？。
  • Pytorch Tutorial仅提供最基本的代码帮助理解BiLSTM-CRF，具体的到实践，该代码还有很大的优化空间。如批次训练、GPU训练、维特比解码和配分函数计算优化等。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
import torch
import torch.autograd as autograd
import torch.nn as nn
import torch.optim as optim

torch.manual_seed(1)

def prepare_sequence(seq, to_ix):
    idxs = [to_ix[w] for w in seq]
    return torch.tensor(idxs, dtype=torch.long)

def argmax(vec):
	# 得到最大的值的索引
	_, idx = torch.max(vec, 1)
	return idx.item()

def log_sum_exp(vec):
	max_score = vec[0, argmax(vec)]  # max_score的维度为1
	max_score_broadcast = max_score.view(1, -1).expand(1, vec.size()[1])  # 维度为1*5
	return max_score + torch.log(torch.sum(torch.exp(vec - max_score_broadcast)))
	#等同于torch.log(torch.sum(torch.exp(vec)))，防止e的指数导致计算机上溢

class BiLSTM_CRF(nn.Module):
	def __init__(self, vocab_size, tag_to_ix, embedding_dim, hidden_dim):
		super(BiLSTM_CRF, self).__init__()
		self.embedding_dim = embedding_dim
		self.hidden_dim = hidden_dim
		self.vocab_size = vocab_size
		self.tag_to_ix = tag_to_ix
		self.tagset_size = len(tag_to_ix)

		self.word_embeds = nn.Embedding(vocab_size, embedding_dim)
		self.lstm = nn.LSTM(embedding_dim, hidden_dim // 2, num_layers=1, bidirectional=True)
		self.hidden2tag = nn.Linear(hidden_dim, self.tagset_size)
		# 转移矩阵，transitions[i][j]表示从label_j转移到label_i的概率,虽然是随机生成的但是后面会迭代更新
		self.transitions = nn.Parameter(torch.randn(self.tagset_size, self.tagset_size))

		self.transitions.data[tag_to_ix[START_TAG], :] = -10000  # 从任何标签转移到START_TAG不可能
		self.transitions.data[:, tag_to_ix[STOP_TAG]] = -10000  # 从STOP_TAG转移到任何标签不可能

		self.hidden = self.init_hidden() # 随机初始化LSTM的输入(h_0, c_0)

	def init_hidden(self):
		return (torch.randn(2, 1, self.hidden_dim // 2),
				torch.randn(2, 1, self.hidden_dim // 2))

	def _forward_alg(self, feats):
		'''
		输入：发射矩阵(emission score)，实际上就是LSTM的输出——sentence的每个word经BiLSTM后，对应于每个label的得分
		输出：所有可能路径得分之和/归一化因子/配分函数/Z(x)
		'''
		init_alphas = torch.full((1, self.tagset_size), -10000.)
		init_alphas[0][self.tag_to_ix[START_TAG]] = 0.

		# 包装到一个变量里面以便自动反向传播
		forward_var = init_alphas
		for feat in feats: # w_i
			alphas_t = []
			for next_tag in range(self.tagset_size): # tag_j
				# t时刻tag_i emission score（1个）的广播。需要将其与t-1时刻的5个previous_tags转移到该tag_i的transition scors相加
				emit_score = feat[next_tag].view(1, -1).expand(1, self.tagset_size) # 1*5
				# t-1时刻的5个previous_tags到该tag_i的transition scors
				trans_score = self.transitions[next_tag].view(1, -1)  # 维度是1*5

				next_tag_var = forward_var + trans_score + emit_score
				# 求和，实现w_(t-1)到w_t的推进
				alphas_t.append(log_sum_exp(next_tag_var).view(1))
			forward_var = torch.cat(alphas_t).view(1, -1) # 1*5

		# 最后将最后一个单词的forward var与转移 stop tag的概率相加
		terminal_var = forward_var + self.transitions[self.tag_to_ix[STOP_TAG]]
		alpha = log_sum_exp(terminal_var)
		return alpha

	def _get_lstm_features(self, sentence):
		'''
		输入：id化的自然语言序列
		输出：序列中每个字符的Emission Score
		'''
		self.hidden = self.init_hidden() # (h_0, c_0)
		embeds = self.word_embeds(sentence).view(len(sentence), 1, -1)
		lstm_out, self.hidden = self.lstm(embeds, self.hidden)
		lstm_out = lstm_out.view(len(sentence), self.hidden_dim)
		lstm_feats = self.hidden2tag(lstm_out) # len(s)*5
		return lstm_feats

	def _score_sentence(self, feats, tags):
		'''
		输入：feats——emission scores；tags——真实序列标注，以此确定转移矩阵中选择哪条路径
		输出：真实路径得分
		'''
		score = torch.zeros(1)
		# 将START_TAG的标签３拼接到tag序列最前面
		tags = torch.cat([torch.tensor([self.tag_to_ix[START_TAG]], dtype=torch.long), tags])
		for i, feat in enumerate(feats):
			score = score + \
					self.transitions[tags[i + 1], tags[i]] + feat[tags[i + 1]]
		score = score + self.transitions[self.tag_to_ix[STOP_TAG], tags[-1]]
		return score

	def _viterbi_decode(self, feats):
		# 预测序列的得分，维特比解码，输出得分与路径值
		backpointers = []

		init_vvars = torch.full((1, self.tagset_size), -10000.)
		init_vvars[0][self.tag_to_ix[START_TAG]] = 0

		forward_var = init_vvars
		for feat in feats:
			bptrs_t = []
			viterbivars_t = []

			for next_tag in range(self.tagset_size):
				next_tag_var = forward_var + self.transitions[next_tag]  # forward_var保存的是之前的最优路径的值
				best_tag_id = argmax(next_tag_var)  # 返回最大值对应的那个tag
				bptrs_t.append(best_tag_id)
				viterbivars_t.append(next_tag_var[0][best_tag_id].view(1))

			forward_var = (torch.cat(viterbivars_t) + feat).view(1, -1)
			backpointers.append(bptrs_t)  # bptrs_t有５个元素

		# 其他标签到STOP_TAG的转移概率
		terminal_var = forward_var + self.transitions[self.tag_to_ix[STOP_TAG]]
		best_tag_id = argmax(terminal_var)
		path_score = terminal_var[0][best_tag_id]

		best_path = [best_tag_id]
		for bptrs_t in reversed(backpointers):
			best_tag_id = bptrs_t[best_tag_id]
			best_path.append(best_tag_id)
		
		# 无需返回最开始的START位
		start = best_path.pop()
		assert start == self.tag_to_ix[START_TAG]
		best_path.reverse()  # 把从后向前的路径正过来
		return path_score, best_path

	def neg_log_likelihood(self, sentence, tags):  # 损失函数
		feats = self._get_lstm_features(sentence)  # len(s)*5
		forward_score = self._forward_alg(feats)  # 规范化因子/配分函数
		gold_score = self._score_sentence(feats, tags) # 正确路径得分
		return forward_score - gold_score  # Loss（已取反）

	def forward(self, sentence):
		'''
		解码过程，维特比解码选择最大概率的标注路径
		'''
		lstm_feats = self._get_lstm_features(sentence)

		score, tag_seq = self._viterbi_decode(lstm_feats)
		return score, tag_seq

START_TAG = "<START>"
STOP_TAG = "<STOP>"
EMBEDDING_DIM = 5 # 由于标签一共有B\I\O\START\STOP 5个，所以embedding_dim为5
HIDDEN_DIM = 4 # 这其实是BiLSTM的隐藏层的特征数量，因为是双向所以是2倍，单向为2

training_data = [(
	"the wall street journal reported today that apple corporation made money".split(),
	"B I I I O O O B I O O".split()
), (
	"georgia tech is a university in georgia".split(),
	"B I O O O O B".split()
)]

word_to_ix = {}
for sentence, tags in training_data:
	for word in sentence:
		if word not in word_to_ix:
			word_to_ix[word] = len(word_to_ix)

tag_to_ix = {"B": 0, "I": 1, "O": 2, START_TAG: 3, STOP_TAG: 4}

model = BiLSTM_CRF(len(word_to_ix), tag_to_ix, EMBEDDING_DIM, HIDDEN_DIM)
optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=1e-4)

for epoch in range(300):
	for sentence, tags in training_data:
		model.zero_grad()
		
        # 输入
		sentence_in = prepare_sequence(sentence, word_to_ix)
		targets = torch.tensor([tag_to_ix[t] for t in tags], dtype=torch.long)
		
        # 获取loss
		loss = model.neg_log_likelihood(sentence_in, targets)
		
        # 反向传播
		loss.backward()
		optimizer.step()

with torch.no_grad():
	precheck_sent = prepare_sequence(training_data[0][0], word_to_ix)
	print(model(precheck_sent))

参考

  1. 流水的NLP铁打的NER：命名实体识别实践与探索
  2. 序列标注方法BIO、BIOSE、IOB、BILOU、BMEWO、BMEWO+的异同
  3. BiLSTM-CRF模型理解
  4. Understanding LSTM Networks
  5. pytorch中LSTM的细节分析理解
  6. ADVANCED: MAKING DYNAMIC DECISIONS AND THE BI-LSTM CRF
  7. 如何通俗地讲解 viterbi 算法？
  8. 命名实体识别（NER）：BiLSTM-CRF原理介绍+Pytorch_Tutorial代码解析_人工智能_misite_J-DevPress官方社区 (csdn.net)
  9. 《统计学习方法（第二版）》